There is more than one aim in our calculations. First, we want to be
able to calculate amplitude spectra of oscillations. In Fig. 1
we show for l=1 to l=4 the normalized amplitude spectra (which are
independent, for small amplitudes, of the often unknown inclination
i; e.g., RKN, BFW). As one can see from Fig. 1, the slope
varies strongly with l. By comparing the observed slope with the
theoretical slope, one can therefore determine l (the slope also
depends on 
and 
, which may have to be
constrained from other observations).
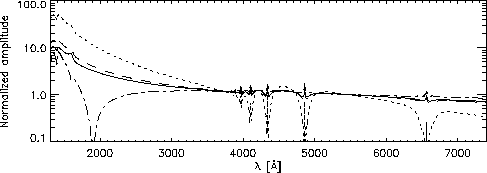
Figure:
Normalized amplitude spectra for l=1 (solid), l=2 (dashed), l=3
(dotted) and l=4 (dash-dotted) modes ( 
,
, 
). Around 1900 Å the phase of the l=4
mode changes by 
, causing the amplitude to go to zero
A second aim of our program is to calculate time-resolved
spectra. This is shown in Fig. 2 for l=1, m=0 for a strong
oscillation resulting in variations of of 
.
One can see that the spectra depend strongly on the
inclination. Furthermore, one can see the effects of having a
distribution of at maximum and minimum instead of a
uniform across the WD surface.
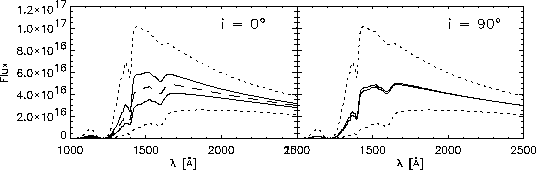
Figure 2:
UV-spectra at maximum and minimum (solid) for l=1, m=0
oscillations with 
for 
(left) and 
(right). Also shown are the equilibrium spectrum
( , 
, ;
dashed) and spectra at 
(dotted)
A third aim is to properly take into account non-linear variations of
I with linear, i.e., sinusoidal, variations of . For
the above case we show in Fig. 3 the light curve for a filter
located near the center of 
and just outside this
line. One can see that the light curve differs strongest from the
underlying pure sinusoidal variation of near the center
of the spectral line. This causes strong amplitudes at higher
harmonics in the Fourier spectrum.
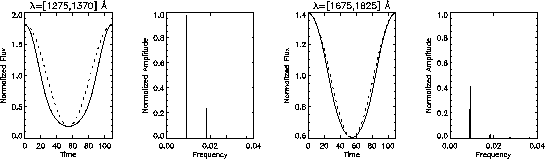
Figure 3:
Light curves and corresponding Fourier spectra for oscillations as in
Fig. 2 with close to the center of the
line (left panels) and just outside the line (right
panels). The underlying sinusoidal variation of is
overplotted (dotted)